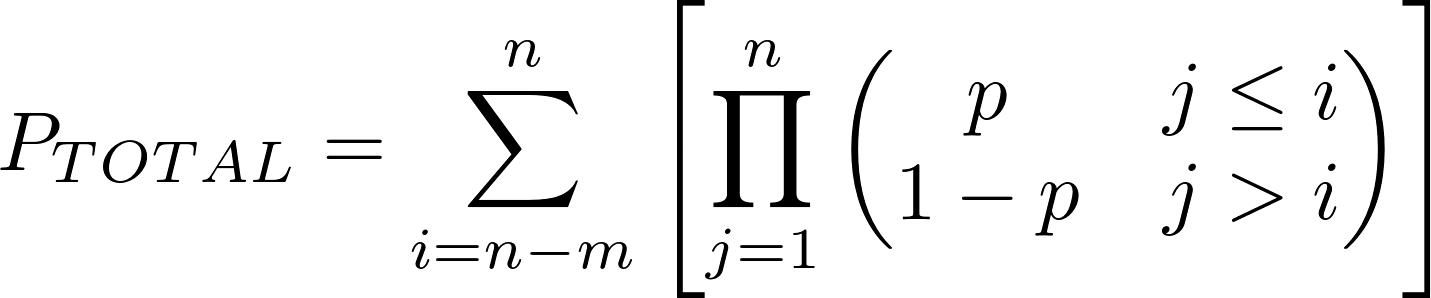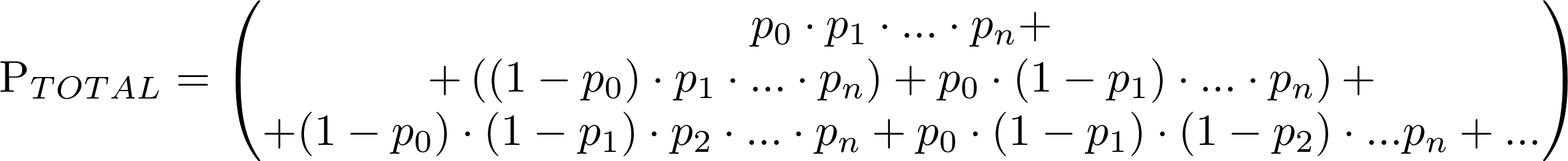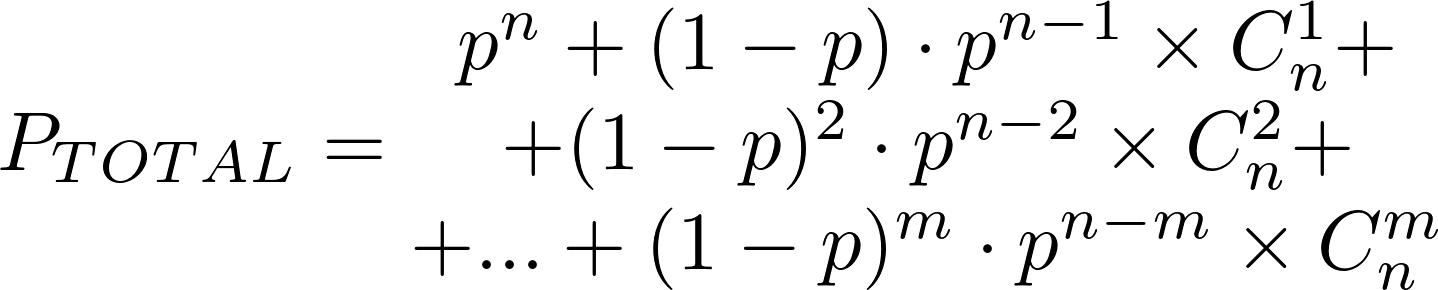Некоторые задачи из теории надёжности

Вероятность выхода из строя в течение заданного времени

В этой расчётной модели закон распределения наработки на отказ переключаемый: экспоненциальный или Вейбулла. Имеется специальная страница, на которой можно поэкспериментировать с исходными величинами и посмотреть область возможных значений случайных величин.

Параметры времени: среднюю наработка, расчётный период времени и время предшествующей наработки устройства - теперь можно вписывать в днях и годах. Для этого надо вписать значения «5 дней» или «20 лет»

Закон распределения: экспоненциальный Эксп.
Вейб.
Средняя наработка на отказ, час
Расчётный период времени, час
Предыдущая наработка, час
Вероятность безотказной работы, %
Вероятность отказа за период, %

Что под капотом? Банальное интегрирование плотности вероятности f(t) в пределах от нуля до момента t, введённого в соответствующее поле. А точнее, просто вычисляется значение функции распределения F(t+τ0) в указанной точке. При учёте предыдущей наработки (τ0 > 0) дополнительно вычисляется F(τ0) и вычисляется условная вероятность того, что отказ произойдёт или не произойдёт в интервале времени T = τ0 ÷ τ0+t, при условии, что в интервале T = 0÷τ0+t отказа не произошло.

Надёжность системы параллельно работающих приборов

Определяется надёжность работы системы, состоящей из n одинаковых устройств, каждое из которых работает с некоторой надёжностью p (или имеет такой коэффициент готовности), допускается выход из строя m устройств без потери работоспособности системы. Определяется вероятность успешной работы всей системы (или коэффициент готовности).

Количество устройств n
Допускается выход из строя m
Вероятность успешной работы устройства p, %
Вероятность успешной работы системы, %

Что под капотом? Классический расчёт вероятности событий:

Показать громоздкие формулы расчёта

Яндекс.Метрика